Logistic regression tutorial

This part of tutorial is derived from its step-by-step notebook version multinomial logistic regression example, the emphasis is to showcase the basic capacity of MinPy.

We will work on a classification problem of a synthetic data set. Each point is a high-dimentional data in one of the five clusters. We will build a one-layer multinomial logistic regression model. The goal is to learn a weight matrix weight, such that for a data point x the probability that it is assigned to its class (cluster) is the largest.

The data is generated with the following code.

import numpy as np

""" Generates several clusters of Gaussian points """
def gaussian_cluster_generator(num_samples=10000, num_features=500, num_classes=5):
    mu = np.random.rand(num_classes, num_features)
    sigma = np.ones((num_classes, num_features)) * 0.1
    num_cls_samples = num_samples / num_classes
    x = np.zeros((num_samples, num_features))
    y = np.zeros((num_samples, num_classes))
    for i in range(num_classes):
        cls_samples = np.random.normal(mu[i,:], sigma[i,:], (num_cls_samples, num_features))
        x[i*num_cls_samples:(i+1)*num_cls_samples] = cls_samples
        y[i*num_cls_samples:(i+1)*num_cls_samples,i] = 1
    return x, y

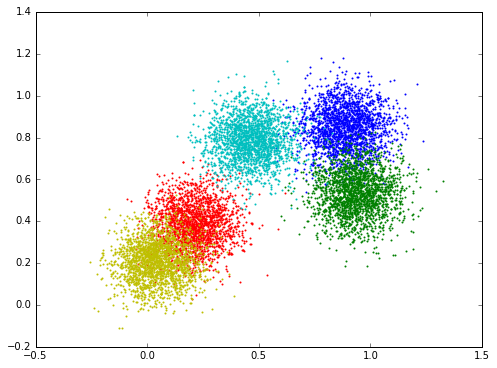
The visualization of the data:

The following is the numpy version. The function predict outputs the probability, the train function iterates over the data, computes the loss, the gradients, and updates the parameters w with a fixed learning rate.

import numpy as np
import numpy.random as random
from examples.utils.data_utils import gaussian_cluster_generator as make_data

# Predict the class using multinomial logistic regression (softmax regression).
def predict(w, x):
    a = np.exp(np.dot(x, w))
    a_sum = np.sum(a, axis=1, keepdims=True)
    prob = a / a_sum
    return prob

# Using gradient descent to fit the correct classes.
def train(w, x, loops):
    for i in range(loops):
        prob = predict(w, x)
        loss = -np.sum(label * np.log(prob)) / num_samples
        if i % 10 == 0:
            print('Iter {}, training loss {}'.format(i, loss))
        # gradient descent
        dy = prob - label
        dw = np.dot(data.T, dy) / num_samples
        # update parameters; fixed learning rate of 0.1
        w -= 0.1 * dw

# Initialize training data.
num_samples = 10000
num_features = 500
num_classes = 5
data, label = make_data(num_samples, num_features, num_classes)

# Initialize training weight and train
weight = random.randn(num_features, num_classes)
train(weight, data, 100)

The minpy version is very similar, except a few lines that are highlighted:

• Among some new imported libraries, minpy.numpy replaces numpy. This lightweight library is fully numpy compatible, but it allows us to add small instrumentations in the style of autograd
• Defines loss explicitly with the function train_loss
• MinPy then derives a function to compute gradients automatically (line 24)

import minpy.numpy as np
import minpy.numpy.random as random
from minpy.core import grad_and_loss
from examples.utils.data_utils import gaussian_cluster_generator as make_data
from minpy.context import set_context, gpu

# Please uncomment following if you have GPU-enabled MXNet installed.
# This single line of code will run MXNet operations on GPU 0.
# set_context(gpu(0)) # set the global context as gpu(0)

# Predict the class using multinomial logistic regression (softmax regression).
def predict(w, x):
    a = np.exp(np.dot(x, w))
    a_sum = np.sum(a, axis=1, keepdims=True)
    prob = a / a_sum
    return prob

def train_loss(w, x):
    prob = predict(w, x)
    loss = -np.sum(label * np.log(prob)) / num_samples
    return loss

"""Use Minpy's auto-grad to derive a gradient function off loss"""
grad_function = grad_and_loss(train_loss)

# Using gradient descent to fit the correct classes.
def train(w, x, loops):
    for i in range(loops):
        dw, loss = grad_function(w, x)
        if i % 10 == 0:
            print('Iter {}, training loss {}'.format(i, loss))
        # gradient descent
        w -= 0.1 * dw

# Initialize training data.
num_samples = 10000
num_features = 500
num_classes = 5
data, label = make_data(num_samples, num_features, num_classes)

# Initialize training weight and train
weight = random.randn(num_features, num_classes)
train(weight, data, 100)

Now, if you uncomment line 9 to set MXNet context on GPU 0, this one line change (set_context(gpu(0))) will enable the same code to run on GPU!

For more functionality of MinPy/MXNet, we invite you to read later sections of this tutorial.